Let's Flip Out...
Take a coin and give it a toss. We all know the odds of it coming up heads (or tails) is exactly 50:50, which is why coin tosses are used to make random binary decisions (only two possible outcomes, such as which team gets the ball first). For the sake of this example, we will consider heads to be the 'lucky' outcome, so we continue to flip the coin to see how 'lucky' we can get. After flipping the coin five times you see it always comes up heads. The odds of this are 1/2 * 1/2 *1/2 *1/2 *1/2 or 1/32 – very lucky indeed! Now, what are the odds of another coin flip also coming up heads? One's intuition screams that this lucky streak can't continue, so the odds must be very steep indeed. But – you would be dead wrong, because the coin has no memory! The odds of coming up heads again are the same as the first toss – exactly 50:50. The part that is hard to get one's head around is that it is the entire sequence that is unlikely, not just a single event. Now, it's time to do an experiment to look at such 'lucky' streaks.
Call In The Urchins!
Let's round up 100 neighborhood kids, give them each a coin, have them toss it twenty times and report
back how many times it comes up heads. The least number of 'lucky' tosses would of course be zero, and
since the coin is tossed twenty times, the maximum number must be 20.
Here are the results that the kids reported:
Jill – 6
James – 14
Tim – 10
Jerry – 9
Amanda – 7
etc, etc...
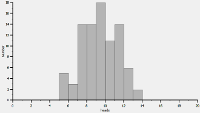 Instead of just reading the list, making up a graph (click
to enlarge) can give us a better picture of what is going on. We can use a series of bars to show how many times
each 'lucky streak' came up, and it looks like the image on the left. The higher the bar, the more times
it occurred, so we can see the number of 'heads' seems highest around 10, and if we actually average all
the results, we get very close to ten (9.9 in this case).
Instead of just reading the list, making up a graph (click
to enlarge) can give us a better picture of what is going on. We can use a series of bars to show how many times
each 'lucky streak' came up, and it looks like the image on the left. The higher the bar, the more times
it occurred, so we can see the number of 'heads' seems highest around 10, and if we actually average all
the results, we get very close to ten (9.9 in this case).
And Then Even More Of Them...
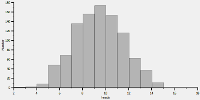 Since it looks like we may be on to something, let's get a government grant and do a
really big study: go to the Caribbean where there are (coincidentally...) a large number of children, find 1000
of them and see how 'lucky' they can be. Their results are shown on the right, and except for looking
smoother, the distribution is about the same. But, we still didn't find anyone who got all 20 heads; the best
one got 15 out of 20, which is still very darned 'lucky'.
Since it looks like we may be on to something, let's get a government grant and do a
really big study: go to the Caribbean where there are (coincidentally...) a large number of children, find 1000
of them and see how 'lucky' they can be. Their results are shown on the right, and except for looking
smoother, the distribution is about the same. But, we still didn't find anyone who got all 20 heads; the best
one got 15 out of 20, which is still very darned 'lucky'.
What these exercises show is that a series of unrelated events (each coin toss doesn't affect another) leads to a number of combinations, some much more likely than others. There is a mathematical measurement of this likelihood, which is called the 'standard deviation' – the more standard deviations away from the norm, the less likelihood of the combination. In this case, the value for this coin toss is a bit over 2.2, so if we go plus or minus 2 standard deviations from the average (of 10), we can compute that about 96% of the little tossers would get between 5.5 and 14.5 heads out of 20. The further we go out (more standard deviations), the less likely an event is. About now, if you are still reading this, you are probably thinking - “so what does this have to do with anything?”. One answer among others, is intelligence.
You Aren't Responsible For This...
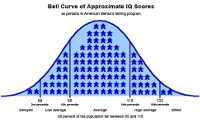 If there was only one factor which determined it, everyone would have the same IQ; if there were
only a few factors, the distribution of IQ values would be either very narrow or it would be 'lumpy',
with several peaks and valleys. However, since there are many factors that determine one's intelligence, it
should not be a surprise to find that the distribution of IQ within a population is similar to that of the coin
tosses, a bell-shaped curve with most values clustered around the center and some extended 'tails' – in
the case of intelligence, the 'too dumb to breathe' and the 'too smart for their own good'
populations. The message here is that your place on this curve was determined by many individual happenings, most
of them beyond your ability to influence in any meaningful way. It is strongly presumed that early childhood
socialization/stimulation will boost IQ in a still-plastic brain, but it is also probable that such stimulation
will only have much effect in those with the requisite 'horsepower'; thus environmental/developmental
effects may largely act to expand inherited differences.
If there was only one factor which determined it, everyone would have the same IQ; if there were
only a few factors, the distribution of IQ values would be either very narrow or it would be 'lumpy',
with several peaks and valleys. However, since there are many factors that determine one's intelligence, it
should not be a surprise to find that the distribution of IQ within a population is similar to that of the coin
tosses, a bell-shaped curve with most values clustered around the center and some extended 'tails' – in
the case of intelligence, the 'too dumb to breathe' and the 'too smart for their own good'
populations. The message here is that your place on this curve was determined by many individual happenings, most
of them beyond your ability to influence in any meaningful way. It is strongly presumed that early childhood
socialization/stimulation will boost IQ in a still-plastic brain, but it is also probable that such stimulation
will only have much effect in those with the requisite 'horsepower'; thus environmental/developmental
effects may largely act to expand inherited differences.
Of course, we are ignoring exactly what the 'IQ' tests actually measure and how sensitive they are to individual, educational or cultural factors, but in general, people with a higher measured IQ do better in school, make more money and even live longer. Regardless of how one feels about IQ tests and their meaning, we can all relate to our life experience that some people quickly 'get it' and others are pretty thick. Frankly, this factor makes it hard for a smart person to have extended conversations with someone who is not, and this leads to assortative mating – smart people more often than not marry smart people. Since studies in identical twins suggest that genetic factors contribute to at least half of one's intelligence, this means the 'tails' of the curves become self-reinforcing from genetics alone, not to mention all the other environmental benefits from being born into a smart family. So – the smart (rich) get smarter and the rest - well, you can guess...
But It Gets Even Worse
 Although one's family and early environment will 'doom' you to a fixed place in the IQ
sweepstakes, you can always find consolation in the fact that 'smarts aren't everything'. However, it
turns out that there are other personal factors which also follow the bell-shaped curve, and these factors
interact with IQ to form a population even more skewed than that created by IQ alone, leaving a society better suited to
earlier forms of governance than those found in our more 'enlightened' times.
Although one's family and early environment will 'doom' you to a fixed place in the IQ
sweepstakes, you can always find consolation in the fact that 'smarts aren't everything'. However, it
turns out that there are other personal factors which also follow the bell-shaped curve, and these factors
interact with IQ to form a population even more skewed than that created by IQ alone, leaving a society better suited to
earlier forms of governance than those found in our more 'enlightened' times.
We will explore these factors at another time....